RECURSOS DE ATENCIÓN (III)

Una extensión de los modos de atención a múltiples recursos se relaciona con la medida de la carga de trabajo mental o las demandas que se le imponen al procesador de información del ser humano. Una defi nición utiliza la relación de los recursos que se requieren y los recursos disponibles, donde el tiempo es uno de los más importantes entre la gran cantidad de recursos que se necesitan.
En los ejemplos que se mencionaron anteriormente, el ensamblado simple puede ser una tarea que consuma mucho tiempo, pero no demanda en particular recursos cognitivos. Por otro lado, el control del tráfi co aéreo, en horas pico, puede ser una tarea muy demandante. En realidad, puede ser muy difícil cuantifi car las demandas impuestas al operador. Algunos de los métodos que se utilizan para cuantifi carlas son las siguientes:

■ Las medidas de la tarea principal pueden ser el tiempo que se requiere para llevar a cabo la tarea dividido entre el tiempo total disponible, o el número de artículos terminados por unidad de tiempo. El problema de este método es que el tiempo compartido de algunas de estas tareas es mejor que el de otras.

■ La medición de la tarea secundaria utiliza el concepto de capacidad de reserva que, si no está directamente relacionada con el desempeño de la tarea principal, será utilizada por la tarea secundaria (tiempo de reacción a la elección), la cual puede ser controlada y más fácilmente medida. El problema de este método es que, por lo general, la tarea secundaria parece artifi cial e intrusiva y que es difícil identifi car la forma en que el operador asigna prioridades al desempeño de ambas tareas.

■ Se piensa que las medidas fi siológicas (por ejemplo, la variabilidad del ritmo cardiaco, el movimiento de los ojos, el diámetro de las pupilas, los electroencefalogramas) responden al estrés impuesto por la carga de trabajo mental; a pesar de que por lo general no interfi eren con el desempeño de la tarea principal, el equipo necesario para medirlas lo puede hacer.

■ Se piensa que las medidas subjetivas agregan todos los aspectos de la carga de trabajo mental en un valor general simple (o en un promedio ponderado en varias escalas). Desafortunadamente, los reportes subjetivos no siempre refl ejan con precisión el desempeño real; también la motivación puede afectar signifi cativamente los valores.

RECURSOS DE ATENCIÓN (II)

Por otro lado, cuando un inspector clasifi ca manzanas en una banda transportadora, divide su atención entre la percepción visual de los defectos y tamaños de las manzanas, la toma de decisiones acerca de la naturaleza del defecto y el tamaño de la manzana, con referencia a la memoria y a las imágenes almacenadas a partir del entrenamiento que recibió, y los movimientos de las manos para quitar las manzanas dañadas y clasifi car por tamaño las que están en buen estado en los contenedores apropiados. A este último caso consistente en realizar varias tareas de manera simultánea también se le conoce como multitarea o compartición del tiempo. Debido a que los recursos cognitivos de la atención están relativamente limitados, la compartición de tiempo entre varias tareas probablemente dará como resultado un deterioro del desempeño de una o más tareas en comparación con una sola de ellas. De nuevo, puede resultar complejo mejorar el desempeño de la tarea en dichas situaciones, pero también se utilizan estrategias similares como las que se estudiaron en el caso de la atención enfocada. El número y grado de difi cultad de las tareas debe minimizarse. Es necesario que las tareas se realicen de la manera más disímil posible en términos de las demandas exigidas a la etapa de procesamiento de la fi gura 7.1. Mientras que una tarea de ensamblado manual sólo con instrucciones auditivas puede llevarse a cabo sin problemas, un músico que esté afi nando un instrumento tendrá problemas para escuchar comentarios verbales. Un método muy exitoso para explicar el desempeño del tiempo compartido con tareas múltiples es el modelo de recursos múltiples de Wickens (1984).

RECURSOS DE ATENCIÓN (I)

Los recursos de atención o, en términos más sencillos, la atención, se refi ere a la cantidad de capacidad cognitiva que se dedica a una tarea en particular o etapa de procesamiento. Dicha cantidad puede variar de manera considerable desde tareas de ensamble rutinarias y bien practicadas con reducidas demandas de atención hasta tareas relacionadas con el control de tráfi co aéreo que exigen un elevado nivel de atención. Además, esta capacidad cognitiva puede aplicarse de una forma muy directa, como en un punto específi co de una parte en particular del sistema de procesamiento de información del ser humano llamada atención enfocada, o, de una manera mucho más difusa a varias o a todo el sistema de procesamiento de información del ser humano, lo cual se llama atención dividida. Un ejemplo de la atención enfocada en la memoria de trabajo se podría presentar mientras un operador trata de recordar un código de procesamiento de consulta mientras lo ingresa en una máquina herramienta controlada por computadora. El enfoque de la atención puede mejorarse si se reduce el número de fuentes de información en competencia o las demandas del sistema de procesamiento de información del ser humano o si se separan dichas fuentes de la manera más distinta posible.

Ley de Fitts y procesamiento de información del movimiento

Fitts (1954), que aplicó la teoría de la información al modelado del movimiento del ser humano, fue quien desarrolló el índice de difi cultad para predecir el tiempo de los movimientos. Este índice se definió en función de la distancia del movimiento y el tamaño del objetivo en una serie de movimientos posicionales hacia y desde objetivos idénticos:

En una aplicación particularmente exitosa de la ley de Fitts, Langolf, Chaffi n y Foulke (1976) modelaron el movimiento humano realizado por diferentes extremidades a lo largo de un gran número de distancias, incluyendo objetivos muy pequeños, visibles sólo con la ayuda de un microscopio.
Sus resultados (vea la fi gura 4.14) arrojaron pendientes de 105 ms/bit para el brazo, 45 ms/bit para la muñeca y 26 ms/bit para el dedo. El valor inverso de la pendiente se interpreta, de acuerdo con la teoría de la información, como el ancho de banda de sistema motor. En este caso, los anchos de banda fueron de 38 bits/s para el dedo, 23 bits/s para la muñeca y 10 bits/s para el brazo. Esta reducción de las velocidades de procesamiento de información se explicó como resultado del procesamiento adicional de las articulaciones, músculos y unidades motoras. Como un detalle interesante, estos resultados son idénticos a la clasifi cación de movimientos de Gilbreth (vea la sección 4.2).

Ejemplo Procesamiento de información del ser humano en una tarea de cableado

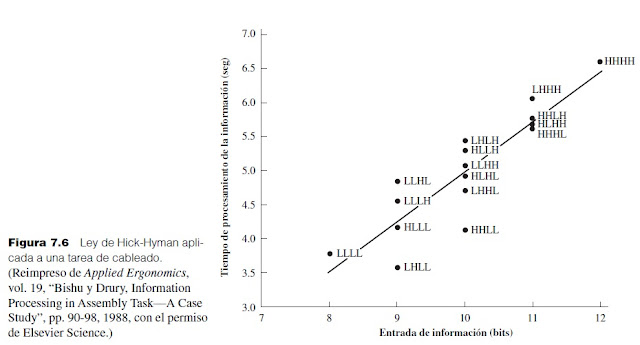
Un buen ejemplo de la cuantifi cación de la cantidad de información procesada en una tarea industrial fue presentado por Bishu y Drury (1988). En una tarea simulada de cableado, los operadores movían un punzón hacia la terminal o ubicación sobre un tablero de control, conformado por cuatro placas diferentes, cada una de las cuales tenía ocho posibles componentes. Cada área de componentes estaba dividida en 128 terminales con un arreglo de ocho columnas y 16 fi las. La tarea más compleja involucraba las cuatro placas (log2 4 = 2 bits de información), los ocho componentes (3 bits), ocho columnas (3 bits) y 16 fi las (4 bits) todo lo cual constituía una complejidad total de 12 bits (suma de 2, 3, 3 y 4). A partir de este panel de control, se pueden construir otros de menor complejidad mediante la reducción del número de placas, componentes, columnas y fi las. Una tarea de baja complejidad sólo involucra dos placas (1 bit), cuatro componentes (2 bits), cuatro columnas (2 bits) y 8 fi las (3 bits) para dar una complejidad total de 8 bits (la suma de 1, 2, 2 y 3). También se consideraron otras tareas de complejidad intermedia.
Los resultados fi nales mostraron una relación lineal entre el tiempo de procesamiento de la información (cableado simulado o colocación) y la complejidad de la información de la entrada (vea la fi gura 7.6). Mediante el uso de la ley Hick-Hyman, esta relación puede expresarse como

Por lo tanto, a medida que aumenta el número de alternativas para realizar la tarea, también reincrementa la carga informacional en la unidad central de proceso del operador humano así como el tiempo correspondiente del desempeño de la tarea. Observe que en este caso de la vida real de una tarea compleja, la intercepción no siempre es un valor positivo correspondiente al simple tiempo de reacción.

EJECUCIÓN DE LA RESPUESTA (I)

La ejecución de la respuesta depende fundamentalmente del movimiento humano. En el capítulo 4 se pueden encontrar más detalles acerca del sistema músculo-esquelético, el control motor y el trabajo manual. Observe que la Tarea de golpes de Fitts (vea la fi gura 7.7) es una simple extensión de la ley de Hick-Hyman respecto al movimiento y también un ejemplo de un compromiso velocidad-precisión con relación al tamaño del tiempo del objetivo y del movimiento. Las aplicaciones específi cas de las respuestas respecto a los controles y a la operación de las máquinas y otros equipos se estudian en el capítulo 5.

TOMA DE DECISIONES Y SELECCIÓN DE LA RESPUESTA (IV)

Observe que cuando sólo existe una opción (por ejemplo, cuando aparezca la luz, presione el botón), H = 0 y el tiempo de respuesta es igual a la intercepción. Esto se conoce como el tiempo de reacción simple, el cual puede variar en función al tipo de estímulo (los tiempos de reacción de la audición son de alrededor de 40 ms más rápidos que los tiempos de reacción visual), la intensidad del estímulo y el estado de preparación de la señal.
Los tiempos de reacción a la elección general también varían de manera considerable debido a una gran cantidad de factores. A medida que crece la compatibilidad (vea también la sección 5.3) entre el estímulo y la respuesta, la respuesta será más rápida. A medida que hay más práctica, la respuesta será más rápida. Sin embargo, a medida que el operador trate de responder más rápido, será mayor el número de errores. De manera similar, si existe un requisito que establezca una presión muy elevada (por ejemplo, en el control del tráfi co aéreo), el tiempo de respuesta se extenderá. A esta relación inversa se le conoce como compromiso velocidad-precisión.

El uso de dimensiones múltiples, otra forma de redundancia, puede también reducir el tiempo de respuesta en la toma de decisiones; o, de forma contraria, si hay información en confl icto, el tiempo de respuesta va a ser más extenso. Un ejemplo clásico es la Tarea color-palabra de Stroop (Stroop, 1935), en la cual se le pide al sujeto que lea una serie de palabras que expresan colores lo más rápido que pueda. En el caso de redundancia de controles, si se le muestra tinta roja y el operador emite la palabra rojo, el sujeto emitirá una respuesta rápida. En el caso confl ictivo, si se le muestran las letras con tinta roja y el operador emite la palabra azul, el tiempo de respuesta se ampliará debido a
confl ictos semánticos y visuales.

TOMA DE DECISIONES Y SELECCIÓN DE LA RESPUESTA (III)

Además, las teorías actuales acerca de la toma de decisiones se centran alrededor de la conciencia situacional, la cual es una evaluación de todas las claves que se reciben del ambiente reinante.
Requiere de la integración de las claves o de la información en representaciones mentales que varían desde un esquema simple hasta modelos mentales complejos. Para mejorar la conciencia situacional, es necesario entrenar a los operadores para reconocer y considerar las claves apropiadas, encontrar inconsistencias dentro de las claves de la situación y analizar y resolver cualquier confl icto que afecte las claves o la situación. Las ayudas para la toma de decisiones, como las tablas simples de decisión (que se analizan en el capítulo 9) o sistemas expertos más complejos pueden ayudar en el proceso de la toma de decisiones. Asimismo, el despliegue de claves importantes, la eliminación de claves indeseables y el uso de técnicas espaciales y la integración de despliegues también pueden ser útiles en este proceso. Algunas de estas técnicas se analizarán en la sección titulada modalidades de despliegue.

La velocidad y difi cultad de la toma de decisiones y la selección de respuestas, como se analizó anteriormente, están infl uenciadas por muchos factores. Por lo general, los intentos por cuantificar este proceso se realizan a través de un experimento elección-tiempo de reacción, en el cual el operador debe responder a varios estímulos con las respuestas apropiadas (vea la fi gura 7.5a). Esto puede considerarse como la toma de decisiones simple y, con base en el sistema de procesamiento de información del ser humano, el tiempo de respuesta debe aumentar a medida que el número de estímulos alternos se incremente. La respuesta es no lineal (vea la fi gura 7.5b), pero cuando la complejidad de la decisión se cuantifi ca en términos de la cantidad de información que contiene en bits, la respuesta se hace lineal y se conoce como ley Hick-Hyman (Hick, 1952; Hyman, 1953; vea la fi gura 7.5c)

TOMA DE DECISIONES Y SELECCIÓN DE LA RESPUESTA (II)

Desafortunadamente, por lo general las personas utilizan una gran variedad de guías heurísticas para tomar decisiones, en cuyo caso una gran cantidad de sesgos pueden infl uir sobre la manera en la que buscamos información, asignamos valores a las salidas y tomamos decisiones generales. Una breve lista de dichos sesgos se puede deducir a partir de Wickens, Gordon y Liu (1997):
■ Se utiliza un número limitado de claves o fragmentos de información.
■ Se le da un peso excesivo a las primeras claves.
■ A las últimas claves no se les presta atención.
■ A las claves prominentes se les asigna un mayor peso.
■ Toda la información se pondera equitativamente sin que importe el peso verdadero.
■ Se genera un limitado número de hipótesis.
■ Una vez que se ha seleccionado una hipótesis, se suprimen las últimas claves.
■ Sólo se vislumbra la información de confi rmación para las hipótesis seleccionadas.
■ Sólo se selecciona un número reducido de respuestas.
■ Se le otorga más importancia a las pérdidas potenciales que a las probables ganancias correspondientes.
Mediante la comprensión de estos sesgos, el ingeniero industrial puede presentar información de una mejor manera y establecer el proceso general para mejorar la calidad de la toma de decisiones y minimizar errores.

TOMA DE DECISIONES Y SELECCIÓN DE LA RESPUESTA (I)

En realidad, la toma de decisiones es la parte medular del procesamiento de información, en la cual las personas evalúan las alternativas y seleccionan la respuesta apropiada. Relativamente, éste es un proceso a largo plazo y debe distinguirse del procesamiento a corto plazo como el tiempo de reacción a la elección. Desafortunadamente, las personas no toman decisiones de manera óptima y, a menudo, no toman decisiones racionales con base en números objetivos o en información general. El método racional de la teoría de decisiones clásica sería el cálculo de un valor esperado con base en la suma de productos de cada resultado multiplicado por su probabilidad esperada:

MEMORIA (IV)

La información de la memoria de trabajo puede transferirse a una memoria de largo plazo en caso de que se necesitara para su uso posterior. Ésta podría ser información relacionada al conocimiento general en la memoria semántica o información acerca de eventos específi cos en la vida de una persona en la forma de memoria de eventos. Dicha transferencia deberá llevarse a cabo de una manera ordenada de tal forma que se puedan recuperar fácilmente los datos en un momento posterior mediante un proceso que conocemos con el nombre de aprendizaje. El proceso de recuperación de información es el enlace débil y puede ser facilitado mediante la activación frecuente de esa ruta de la memoria (por ejemplo, un número del seguro social o telefónico que se utiliza todos los días) y mediante el uso de asociaciones con el conocimiento adquirido con anterioridad. Dichas asociaciones deben ser concretas en lugar de abstractas y llenas de signifi cado para el usuario que utiliza sus expectativas y estereotipos. Por ejemplo, el nombre John Brown puede asociarse con la imagen de una casa café.

Si existe una falta de asociaciones claras y bien organizadas, el proceso puede realizarse de manera artifi cial en la forma de reglas mnemotécnicas ⎯una sigla o una frase⎯, cuyas letras representan una serie de caracteres. Por ejemplo, el código de colores de las resistencias (negro, café, rojo, naranja, amarillo, verde, azul, violeta, gris, blanco) puede recordarse a partir de las primeras letras de cada palabra en la expresión “big brown rabbits often yield great big vocal groans when gingerly slapped”. La estandarización de procedimientos o el uso de las ayudas de la memoria (signos o notas) en procedimientos complejos también ayudan mediante la reducción de la carga en la memoria de largo plazo. Desafortunadamente, la memoria de largo plazo decae de manera exponencial, y su reducción es más signifi cativa en los primeros días. Debido a esto, la efi cacia de los programas de entrenamiento no debe evaluarse inmediatamente después de su impartición.

MEMORIA (III)

La memoria de trabajo se deteriora muy rápido, a pesar del ensayo o el reciclado en serie de los números que se quieren recordar. A medida que haya más números en la memoria de trabajo, tomará más tiempo reciclarlos y será mayor la probabilidad de que se pierdan uno o más de ellos. Se ha calculado que la vida media del almacenamiento en memoria de tres números es de 7 segundos. Lo anterior se puede demostrar fácilmente presentando a un sujeto tres números aleatorios (por ejemplo, 5 3 6). Después de contar hacia atrás 7 segundos con el fi n de evitar el ensayo, la mayoría de las personas han olvidado al menos un número, si no es que dos.
Algunas recomendaciones para reducir errores en las tareas que requieren el uso de la memoria de trabajo (Wickens, Gordon y Liu, 1997) son:
■ Minimizar la carga de memoria en términos de capacidad y del tiempo para conservar el recuerdo.
■ Utilizar la fragmentación, especialmente en términos de las secuencias con signifi cado y el uso de letras respecto a los números (por ejemplo, el uso de palabras o siglas en lugar de números en el caso de números telefónicos libres de pago como, por ejemplo, 1-800-CTD-HELP).
■ Mantenga los fragmentos de tamaño reducido de no más de tres o cuatro caracteres de naturaleza arbitraria.
■ Evite mezclar números con letras (es decir, los fragmentos deben contener caracteres similares).
■ Minimice la confusión que surge de propiciar caracteres con sonidos similares (por ejemplo, las letras D, P y T se confunden fácilmente, contrariamente a lo que sucede con las letras J, F y R).

MEMORIA (II)

Contrariamente a la memoria de largo plazo, la memoria de trabajo representa un medio de almacenamiento temporal de información o de conservarla activa mientras es procesada para obtener una respuesta. Por lo tanto, a veces se le conoce como memoria de corto plazo. Buscar un número telefónico en el directorio y retenerlo hasta que éste haya sido marcado y encontrar un código de procesamiento en una lista y teclearlo en el tablero de control de una máquina representan buenos ejemplos de la memoria de trabajo. La memoria de trabajo tiene límites en cuanto a la cantidad de información y la longitud del tiempo que pueden conservarse los datos.

El límite superior de la capacidad de la memoria de trabajo es de aproximadamente 7 ± 2 números, a lo cual se le conoce a menudo como la regla de Miller en honor al psicólogo que la defi nió (Miller, 1956). Por ejemplo, recordar los 11 dígitos 12125551212 sería muy difícil si no es que imposible.
La capacidad de recordar puede mejorarse mediante la fragmentación, es decir, el agrupamiento de números similares. Cuando los números que se mencionaron con anterioridad se agrupan como 1-212-555-1212, se pueden recordar mucho más fácilmente como tres grupos (el 1 es el estándar

para llamar de larga distancia). De manera similar, mediante el ensayo o la repetición mental de los números, lo cual consume más recursos adicionales de atención (vea la fi gura 7.1) de la memoria de trabajo, se puede mejorar la capacidad de recordar.

Ejemplo Teoría de la detección de señales aplicada a la inspección de vidrio (IV)

Debido al incremento de la sensibilidad, hay un mejor desempeño para identificar partes defectuosas.
A veces, la tasa de éxitos se grafi ca contra la tasa de falsas alarmas con el fi n de obtener una curva característica del operador receptor en la cual la desviación de la curva respecto a la pendiente de 45 grados indica la sensibilidad.
En el estudio del caso de Drury y Addison (1973), se recolectaron datos semanales respecto a la inspección del vidrio a partir de los cuales se calculó el valor de d ′. Un cambio en la política de inspección consistente en proporcionar retroalimentación al inspector general más rápidamente dio como resultado que se incrementara d ' de un valor medio de 2.5 a uno de 3.16, lo cual representa un incremento de 26% en la sensibilidad a lo largo de 10 semanas (vea la fi gura 7.4). Esto representó un incremento de 60% de la relación señal a ruido (es decir, de beta) y una reducción de 50% de la probabilidad de no detectar un defecto.

Ejemplo Teoría de la detección de señales aplicada a la inspección de vidrio (III)

Caso 3: Inspector arriesgado.

Un inspector arriesgado (fi gura 7.3c) establece el criterio alejado hacia la izquierda, lo cual incrementa la probabilidad de éxitos (por ejemplo, 0.95) a expensas de una elevada probabilidad de falsas alarmas (por ejemplo 0.70). En este caso, para la curva de la señal, una probabilidad de 0.95 da una z de 1 – 1.645 y una ordenada de 0.103. En el caso de esta curva de ruido, una probabilidad de 0.70 nos da una z de – 0.524 y una ordenada de 0.348. Beta, entonces, se convierte en 0.296 (0.103/0.348).

Caso 4: Sensibilidad incrementada.

La sensibilidad puede calcularse como la diferencia del valor de z de la misma abscisa de ambas curvas, de la señal y del ruido (fi gura 7.3):
d ′ = z (falsas alarmas) – z (éxitos)

Ejemplo Teoría de la detección de señales aplicada a la inspección de vidrio (II)

En el caso de la curva de señal, una probabilidad de 0.30 arroja una z de 0.524 y una ordenada de 0.348. En el caso de la curva de ruido, la probabilidad de 0.05 da una z de 1.645 y una ordenada de 0.103. Beta, entonces, es igual a 3.38 (0.348/0.103). Observe que la probabilidad de éxitos y fracasos es igual a 1.0 (es decir, 0.30 + 0.70 = 1.0). Lo mismo es válido en el caso de las falsas alarmas y los rechazos correctos.

Caso 2: Inspector promedio.

Si el inspector es promedio ⎯ni conservador ni arriesgado⎯, la probabilidad de éxitos es aproximadamente igual a la probabilidad de rechazos correctos (figura 7.3b). Las curvas se intersecan simétricamente, lo que da como resultado los mismos valores de ordenada y un valor de 1.0 para beta.

Ejemplo Teoría de la detección de señales aplicada a la inspección de vidrio (I)

Una buena aplicación de la teoría de detección de señales fue detallada por Drury y Addison (1973) en la inspección visual del vidrio. La inspección se desarrolló en dos etapas: 1) la inspección general de 100% en la que cada artículo era aceptado o rechazado y 2) una inspección muestral con la ayuda de examinadores especiales quienes reexaminaban los resultados anteriores y suministraban retroalimentación a los inspectores generales. Con base en la calidad de los artículos que se inspeccionaban, una parte estaban bien y los demás estaban defectuosos. El inspector general sólo pudo tomar dos decisiones: aceptar o rechazar. Las respuestas apropiadas podrían ser aceptar un artículo bueno (éxito) y rechazar uno defectuoso (corregir el rechazo). Sin embargo, algunos artículos buenos podrían ser rechazados (fracasos) y algunos artículos defectuosos podrían ser aceptados (falsas alarmas).

Considere cuatro casos diferentes con condiciones variables.
Caso I: Inspector conservador. Un inspector conservador establece el criterio alejado hacia la derecha (fi gura 7.3a). En dicha situación, la probabilidad de éxitos (diciendo sí a la señal del vidrio bueno) es baja (por ejemplo, de 0.30). La probabilidad de falsas alarmas (diciendo sí al ruido del vidrio defectuoso) es aún menor (por ejemplo, de 0.05). Beta se determina mediante la relación entre las ordenadas de la curva de la señal y la curva de ruido en el criterio. La ordenada de una curva normal estándar es

MEMORIA (I)

Una vez que el estímulo ha sido codifi cado de forma sensorial, éste va a la memoria de trabajo, uno de los tres componentes del sistema humano de la memoria. Los otros dos son el almacén sensorial y la memoria de largo plazo. Cada canal sensorial cuenta con un mecanismo de almacenamiento temporal que prolonga el estímulo para que pueda codifi carse correctamente. Este almacenamiento es muy breve, del orden de 1 o 2 segundos, lo cual depende del canal sensorial, antes de que la representación del estímulo desaparezca. También está muy automatizado, en el sentido de que su mantenimiento no requiere de mucha atención. Por otro lado, puede hacerse muy poco para conservar este almacenamiento o aumentar la longitud del lapso que se considere. Observe también en la fi gura 7.1 que, a pesar de que puede haber una gran cantidad de estímulos, lo cual podría representarse en el orden de millones de bits de información ingresando al almacén sensorial, en realidad sólo una porción muy pequeña de dicha información se codifi ca y envía a la memoria de trabajo.
Contrariamente a la memoria de largo plazo, la memoria de trabajo representa un medio de almacenamiento temporal de información o de conservarla activa mientras es procesada para obtener una respuesta. Por lo tanto, a veces se le conoce como memoria de corto plazo. Buscar un número telefónico en el directorio y retenerlo hasta que éste haya sido marcado y encontrar un código de procesamiento en una lista y teclearlo en el tablero de control de una máquina representan buenos ejemplos de la memoria de trabajo. La memoria de trabajo tiene límites en cuanto a la cantidad de información y la longitud del tiempo que pueden conservarse los datos.

TEORÍA DE LA PERCEPCIÓN Y DE LA DETECCIÓN DE SEÑALES (V)

Un segundo concepto de importancia en SDT es la sensibilidad o resolución del sistema sensorial.
En SDT, la sensibilidad se mide como la separación entre las dos distribuciones que se muestran en la fi gura 7.2 y se identifi can como d ′. A medida que la separación sea mayor, mayor será la sensibilidad del observador y las respuestas correctas (más éxitos y más rechazos correctos) y se cometerá un menor número de errores (menos falsas alarmas y fracasos). En general, la sensibilidad mejorará a medida que haya más entrenamiento y vigilancia (por ejemplo, a través de descansos más frecuentes) por parte del inspector, una mejor iluminación en la estación de trabajo y la reducción de la velocidad de la presentación de las señales (la cual conlleva reducir la productividad). Otros factores que pueden ayudar a aumentar la sensibilidad están relacionados con el suministro de patrones visuales de partes defectuosas y la posibilidad de ofrecer un conocimiento de los resultados. Observe que ofrecer incentivos ayudará a incrementar el número de éxitos. Sin embargo, esto es particularmente válido debido a un desplazamiento del sesgo de la respuesta (no de un incremento de la sensibilidad) con un correspondiente aumento del número de falsas alarmas. De manera similar, introducir “señales falsas” para incrementar la vigilancia dará como resultado una mayor tendencia a desplazar el sesgo de la respuesta. En Green y Swets (1988) se puede encontrar más información acerca de la teoría de detección de señales.