DISEÑO DE LAS PARTES - III

DISEÑO DE LAS PARTES - II

De la misma forma en que existen oportunidades para mejorar la productividad mediante un mejor diseño del producto, también la hay para mejorar el diseño de los formatos (ya sea en papel o en formato digital) que se utilizan en la industria y en los negocios. Una vez que se ha determinado la necesidad de un formato, debe estudiarse con el fi n de mejorar la recolección y el fl ujo de información. Los siguientes criterios se aplican en el desarrollo de formatos: 

1. Su diseño debe ser simple, lo que implica, entre otros aspectos, conservar la cantidad de información de entrada necesaria en un nivel mínimo. 

2. Proporcionar sufi ciente espacio para cada bit de información para permitir su ingreso a través de varios métodos (escritura a mano, máquina, procesador de palabras).

3. La secuencia de la entrada de información se debe realizar a través de un patrón lógico. 

4. El formato debe contar con un código de colores que facilite la distribución y el enrutamiento. 

5. Limitar los formatos de computadora a una sola página.

DISEÑO DE LAS PARTES - I

Con frecuencia, los ingenieros de métodos se inclinan a pensar que una vez que ha sido aceptado un diseño, su único recurso es planear su fabricación de la manera más económica posible. Mientras que la introducción de un ligero cambio en el diseño puede ser difícil, un buen analista de métodos debe revisar cada diseño con el fi n de introducirle posibles mejoras. Los diseños pueden modifi carse y si dicho cambio da como resultado una mejora y la actividad que implica realizar la tarea es considerable, se debe proseguir con el cambio. 

Para mejorar el diseño, los analistas deben tener en cuenta los siguientes aspectos con el fi n de reducir el costo de los diseños de cada componente y subensamble: 

1. Reducir el número de partes mediante la simplifi cación del diseño. 

2. Reducir el número de operaciones y la distancia de los recorridos en el proceso de manufactura mediante la unión más efi ciente de las partes y la simplifi cación del maquinado y del ensamblado. 

3. Utilizar materiales de mejor calidad. 

4. Ampliar las tolerancias y confi ar en las operaciones clave para obtener precisión, en lugar de confi ar en una serie de límites muy estrictos. 

5. Realizar los diseños para mejorar la fabricación y el ensamblado. 

Observe que las primeras dos ayudarán a reducir los desperdicios resultado de procesamientos inadecuados, del transporte innecesario y del exceso de inventario. 

General Electric resumió las ideas para desarrollar diseños a un mínimo costo tal como se muestra en la tabla 3.2. 

Los siguientes ejemplos de mejora de métodos se lograron a partir de emplear un mejor material o proceso en un esfuerzo para mejorar el diseño. Las cajas de cables se construyeron originalmente de acero fundido. El diseño mejorado, que representa una caja de cables más resistente, más atractiva, más ligera y menos costosa fue posible gracias al empleo de acero laminado en su fabricación. Se utilizó un proceso de cuatro etapas para doblar las partes en la forma correcta (vea la fi gura 3.2), el cual fue inefi ciente y tensionó el metal en los dobleces. El diseño fue alterado ligeramente de tal manera que pudo utilizarse un proceso de extrusión menos costoso. Las secciones extraídas fueron posteriormente cortadas a la longitud deseada. Durante el rediseño, se eliminaron tres etapas. 

La simplifi cación del diseño a través de la unión más efi ciente de las partes se puso en práctica en el ensamblado de los sujetadores terminales a sus conductores de unión. La práctica original requirió torcer el extremo del sujetador para formar una base. La base se llenó de soldadura, posteriormente el alambre conductor se cubrió con estaño, se insertó en la base llena de soldadura y fue mantenida en esa posición hasta que la soldadura se solidifi có. El diseño modifi cado fue más resistente pues se soldó el sujetador al alambre conductor, lo cual eliminó las operaciones de formado y de hundimiento. La parte original se diseñó con tres componentes que tuvieron que ensamblarse (vea fi gura 3.3). Un método signifi cativamente menos costoso utilizó un diseño de una pieza que pudo maquinarse como una pieza sólida, lo que eliminó dos componentes y varias operaciones.

FINALIDAD DE LA OPERACIÓN - III

Otro ejemplo: en una fábrica de grandes engranes fue necesario incluir una operación para remover y limpiar manualmente con el fi n de quitar las ondulaciones que se formaban en los dientes después de que éstos habían sido puestos al fuego. Una investigación permitió ver que la contracción y expansión generadas por cambios de temperatura en el curso del día eran responsables de esos defectos. Luego de cerrar herméticamente la planta e instalar un sistema de aire acondicionado en el depósito, la compañía pudo mantener la temperatura adecuada durante todo el día. Las ondas desaparecieron de inmediato y ya no fue necesario continuar con las operaciones de remoción y limpieza manual. Para eliminar una operación, los analistas deben preguntar y responder la pregunta siguiente: ¿Puede un proveedor externo realizar la operación de manera más económica? 

Por ejemplo: se compraron cojinetes circulares a un proveedor externo, a los cuales se les tuvo que untar grasa antes de ser ensamblados. Un estudio de proveedores de cojinetes reveló que cojinetes “sellados de por vida” podían comprarse a otro proveedor a un menor precio.

Los ejemplos proporcionados en esta sección destacan la necesidad de establecer el propósito de cada operación antes de darse a la tarea de mejorar ésta. Una vez que se ha determinado la necesidad de la operación, los nueve pasos restantes del análisis de operaciones deben ayudar a determinar cómo debe mejorarse.

FINALIDAD DE LA OPERACIÓN - II

FINALIDAD DE LA OPERACIÓN - I

Éste quizá represente el punto más importante de los nueve que conforman el análisis de operaciones. La mejor manera de simplifi car una operación es vislumbrar alguna forma de obtener los mismos o mejores resultados sin que ella implique costos adicionales. Una regla de gran importancia del analista es tratar de eliminar o combinar una operación antes de tratar de mejorarla. De acuerdo con nuestra experiencia, alrededor de 25% de las operaciones que se llevan a cabo pueden eliminarse si se invierte sufi ciente tiempo en el estudio del diseño y del proceso.

Ello también implica la eliminación de los desperdicios (muda) asociados con procesamientos inapropiados. En la actualidad se realiza mucho trabajo innecesario. En muchos casos, la tarea o el proceso no deben simplifi carse o mejorarse, sino que se deben eliminar por completo. La eliminación de una actividad ahorra dinero en la instalación de un método mejorado y no hay interrupción o retraso debido a que no se debe desarrollar, probar o instalar ningún método mejorado. Los operadores no necesitan recibir ninguna clase de entrenamiento sobre el nuevo método y se minimiza la resistencia al cambio cuando se elimina una actividad o tarea innecesaria. 

Respecto al papeleo administrativo, antes de que se desarrolle un formato para la transferencia de información, los analistas deben preguntarse si en realidad es necesario un formato. En la actualidad, los sistemas controlados por computadora pueden reducir la generación de formatos y el trabajo administrativo. Con frecuencia, las operaciones innecesarias son producto de una planeación inadecuada cuando la tarea se hace por primera vez. Una vez que se ha establecido una rutina estándar, es difícil cambiarla, aun si dicho cambio elimina una parte del trabajo y lo vuelve más sencillo. 

Cuando se planean nuevos trabajos, el encargado de la planeación debe incluir una operación extra si existe alguna posibilidad de que el producto sea rechazado sin ella. Por ejemplo, en el torneado de un eje de acero, si surge una pregunta en cuanto a realizar dos o tres cortes para conservar un acabado de 40 micropulgadas, la persona encargada de la planeación invariablemente especifi ca tres cortes, a pesar de que el mantenimiento apropiado de las herramientas de corte complementado con las velocidades y los alimentadores ideales permitan que el trabajo se lleve a cabo sólo con dos cortes. 

A menudo, las operaciones innecesarias se llevan a cabo debido al desempeño inadecuado de las operaciones anteriores. Se debe realizar una segunda operación para “darle un retoque” o hacer aceptable el trabajo realizado en ellas. En una planta, por ejemplo, unas armaduras colocadas en una instalación eran rociadas con pintura , lo que imposibilitaba cubrir el fondo de la armadura con pintura debido a que la instalación impedía que el chorro de pintura llegara hasta él. 

Por lo tanto, era necesario darle un retoque a los fondos de la armadura después de que se habían pintado. Un estudio de este trabajo trajo como consecuencia un rediseño de la instalación que mantenía a la armadura, lo que permitió una cobertura total. Además, una nueva base hizo posible pintar siete armaduras de manera simultánea, mientras que con el viejo método sólo se podía pintar una a la vez. Por lo tanto, considerando que una operación innecesaria se pudo haber desarrollado debido al funcionamiento inadecuado de la operación anterior, el analista pudo eliminar la operación de retoque (vea la fi gura 3.1).

Análisis de operaciones

PUNTOS CLAVE

• Uso del análisis de operaciones para mejorar el método preguntando qué.

• Enfoque en el propósito de la operación preguntando por qué.

• Enfoque en el diseño, materiales, tolerancias, procesos y herramientas preguntando cómo.

• Enfoque en el operador y en el diseño del trabajo preguntando quién.

• Enfoque en la distribución del trabajo preguntando dónde.

• Enfoque en la secuencia de manufactura preguntando cuándo.

• Siempre trate de simplifi car mediante las operaciones de eliminación, combinación y redistribución.

Los analistas de métodos utilizan el análisis de operaciones para estudiar todos los elementos productivos y no productivos de una operación, incrementar la productividad por unidad de tiempo y reducir los costos unitarios con el fi n de conservar o mejorar la calidad. Cuando se utiliza adecuadamente, el análisis de métodos desarrolla un mejor método para hacer el trabajo mediante la simplifi cación de procedimientos operativos y manejo de materiales y la utilización del equipo de una manera más efi caz. 

Por lo tanto, las compañías pueden incrementar la producción y reducir los costos unitarios; garantizar la calidad y reducir la mano de obra defectuosa; e incrementar el entusiasmo del operador a través de las mejoras a las condiciones de trabajo, la minimización de la fatiga y la obtención de salarios más atractivos. El análisis de operaciones es la tercera etapa del método. En ella se lleva a cabo el análisis y se cristalizan los diferentes componentes del método propuesto. Inmediatamente después se obtienen y presentan los hechos mediante el uso de una gran variedad de herramientas útiles para elaborar los diagramas de fl ujo de procesos que se muestran en el capítulo 2. El analista debe revisar cada operación e inspección que se presenta gráfi camente en estos diagramas y realizar una serie de preguntas, la más importante de ellas es por qué: 

1. ¿Por qué es necesaria esta operación? 

2. ¿Por qué esta operación se lleva a cabo de esta manera? 

3. ¿Por qué estas tolerancias son tan estrechas? 

4. ¿Por qué se ha especifi cado este material? 

5. ¿Por qué se ha asignado para hacer el trabajo a esta clase de operador? 

La pregunta por qué de inmediato sugiere otras, entre las que se incluyen cómo, quién, dónde y cuándo.

Por lo tanto, los analistas se pueden preguntar 

1. ¿Cómo puede llevarse a cabo esta operación de una manera mejor? 

2. ¿Quién puede realizar mejor esta operación? 

3. ¿Dónde puede realizarse la operación a un menor costo o con una mayor calidad? 

4. ¿Cuándo debe realizarse la operación para invertir la menor cantidad de manejo de materiales?

Por ejemplo, en el diagrama de procesos operativos que se muestra en la fi gura 2.7, los analistas se podrían formular las preguntas que se muestran en la tabla 3.1 con el fi n de determinar qué tan prácticas son las mejoras que se quieren incorporar a los métodos. La respuesta a estas preguntas ayuda a iniciar la eliminación, combinación y simplifi cación de las operaciones. Asimismo, cuando obtienen las respuestas a dichas preguntas, los analistas se hacen más conscientes de la existencia de otras preguntas que pueden conducir a diversas mejoras. Las ideas parecen generar más ideas, y los analistas con experiencia por lo general pueden plantearse otras posibilidades de mejora. Por lo tanto, siempre deben conservar la mente abierta, de tal manera que los fracasos anteriores no los desilusionen e insistir en probar nuevas ideas. Por lo general, dichas oportunidades para mejorar los métodos se presentan en cada planta con los consecuentes resultados benéfi cos. 

Observe que una parte signifi cativa de la información que se presenta en el capítulo 3 se utiliza en la actualidad en un formato integrado que se llama manufactura esbelta. Ésta se originó en la Toyota Motor Company como una forma de eliminar el desperdicio en el periodo inmediatamente después del embargo petrolero de 1973 y siguió los pasos del sistema Taylor de administración científi ca pero de una manera mucho más amplia, pues se enfocó no sólo en los costos de manufactura, sino que también en los costos de ventas, administrativos y de capital. Los puntos importantes del Sistema de Producción Toyota (TPS) incluyen siete tipos de desperdicio (Shingo, 1987): 1) sobreproducción, 2) espera del siguiente paso, 3) transporte innecesario, 4) procesamiento innecesario, 5) exceso de inventario, 6) movimiento innecesario y 7) productos defectuosos. Las coincidencias con los métodos convencionales se ejemplifi can mediante lo siguiente: 1) las pérdidas en esperas y en transporte representan elementos que se deben examinar y eliminar mediante análisis de diagramas de fl ujo de procesos, 2) el desperdicio de movimiento resume el trabajo de toda la vida de Gilbreth acerca del estudio de movimientos, el cual culmina en los principios del diseño del trabajo y la economía de movimientos, 3) la pérdida de la sobreproducción y el exceso de inventarios están basados en los requerimientos adicionales de almacenamiento para trasladar artículos dentro y fuera de la bodega y 4) los desperdicios que implican los productos defectuosos representa una pérdida pues generan basura o necesitan retrabajos.

Herramientas para la solución de problemas - PROBLEMAS

1. Con base en la tabla de costos de ruptura que se presenta a continuación, ¿cuál será el tiempo mínimo para terminar el proyecto descrito en la fi gura 2.4, cuyos costos normales se muestran en la tabla 2.2? ¿Cuál sería el costo adicional para terminar el proyecto dentro de este periodo? 

2. El tiempo de maquinado por pieza es de 0.164 horas y el tiempo de carga de la máquina es de 0.038 horas. Con un salario del operador de $12.80/hora y un costo de máquina de $14/hora, calcule el número óptimo de máquinas que produzca el costo más bajo por unidad de producción. 

3. En la Dorben Company se le asigna a un trabajador la operación de varias máquinas. Cada una de ellas está fuera de servicio en tiempos aleatorios durante el día. Un estudio muestra del trabajo indica que, en promedio, las máquinas trabajan desatendidas 60% del tiempo. El tiempo de atención del operador a intervalos irregulares promedio es del 40%. Si el costo de la máquina es de $20/hora y el salario del operador es de $12/hora, ¿cuál será el número más favorable de máquinas (desde el punto de vista económico) que deba operar un empleado?

4. El analista en la Dorben Company desea asignar un número de equipos similares a un operador con base en la minimización del costo por unidad de producción. Un estudio detallado de los equipos revela lo siguiente:
Tiempo estándar de la carga de la máquina = 0.34 minutos
Tiempo estándar de la descarga de la máquina = 0.26 minutos
Tiempo de recorrido entre las dos máquinas = 0.06 minutos
Salario del operador = $12.00/hora
Tarifa de la máquina (ociosa y trabajando) = $18.00/hora
Tiempo de alimentación de energía = 1.48 minutos
¿Cuántas máquinas deben asignarse a cada operador?

Herramientas para la solución de problemas - PREGUNTAS

1. ¿Qué muestra el diagrama de procesos operativos?

2. ¿Qué símbolos se utilizan en la construcción del diagrama de procesos operativos?

3. ¿Cómo muestra el diagrama de procesos operativos los materiales introducidos en el fl ujo general?

4. ¿De qué forma el diagrama de fl ujo de procesos difi ere del diagrama de procesos operativos?

5. ¿Cuál es el propósito principal del diagrama de fl ujo de procesos?

6. ¿Qué símbolos se utilizan en la construcción de un diagrama de fl ujo de procesos?

7. ¿Por qué es necesario construir diagramas de proceso a partir de la observación directa, en contraste

con la información que obtiene el encargado?

8. En la construcción de diagrama de fl ujo de procesos, ¿qué método puede utilizarse para calcular las

distancias recorridas?

9. ¿Cómo pueden determinarse los tiempos de retraso en la construcción del diagrama de fl ujo de procesos?

10. ¿Cómo podría usted abogar por el uso del diagrama de fl ujo?

11. ¿Cómo puede mostrarse en el diagrama de fl ujo el fl ujo de varios productos diferentes?

12. ¿Qué par de símbolos del diagrama de fl ujo se utilizan exclusivamente en el estudio de la documentación?

13. ¿Cuáles son las limitaciones de los diagramas de fl ujo de procesos y de procesos operativos y del diagrama de fl ujo?

14. Explique cómo el diagrama PERT puede ahorrar dinero a la compañía.

15. ¿Cuál es el propósito de la ruptura?

16. ¿Cuándo es recomendable construir un diagrama de procesos hombre-máquina?

17. ¿Qué es el acoplamiento de máquinas?

18. ¿De qué manera se benefi cia un operador a través del acoplamiento de máquinas?

19. ¿De qué manera difi ere el diagrama de procesos de grupo del diagrama de procesos hombre-máquina?

20. En una planta de procesos, ¿cuáles de los siguientes diagramas de proceso tienen una mayor aplicación:

el del trabajador y de las máquinas, el de grupo, el operativo, el de fl ujo o recorrido? Explique

su respuesta.

Herramientas para la solución de problemas - RESUMEN

Los diferentes diagramas que se muestran en este capítulo son herramientas muy valiosas para presentar y resolver problemas. De la misma manera en que existen varios tipos de herramientas para realizar trabajos en particular, también se cuenta con diversos diseños de diagramas que pueden ayudar a resolver problemas de ingeniería. 

Los analistas deben comprender las funciones específi cas de cada diagrama de proceso y seleccionar el adecuado para resolver un problema específi co y mejorar las operaciones. El análisis de Pareto y los diagramas de pescado se utilizan para seleccionar una operación crítica y para identifi car las causas raíz y los factores que contribuyen a generar el problema. Los diagramas de Gantt y PERT son herramientas de programación de proyectos. El diagrama de Gantt sólo proporciona un panorama claro, mientras que los diagramas de PERT cuantifi can las interacciones entre las diferentes actividades. La guía para el análisis trabajo-sitio de trabajo se utiliza fundamentalmente en un recorrido físico para identifi car los factores clave relacionados con el trabajador, la tarea, el ambiente y la administración que pueden provocar problemas potenciales. 

El diagrama de procesos de operación proporciona un buen panorama de las relaciones entre las diferentes operaciones e inspecciones en ensamblados que involucran varios componentes. El diagrama de fl ujo del proceso proporciona más detalles para el análisis de las operaciones de manufactura, para encontrar costos ocultos o indirectos, tales como el tiempo de retardo, costos de almacenamiento y costos relacionados con el manejo de materiales. 

El diagrama de fl ujo o recorrido representa un complemento útil para el diagrama de fl ujo del proceso en el desarrollo de las confi guraciones de la planta. Los diagramas de procesos hombre-máquina y de grupo muestran las máquinas o equipos en conjunto con el operador u operadores, y se utilizan en el análisis del tiempo ocioso del operador y del tiempo ocioso de la máquina. Se utilizan cálculos de servicios sincrónicos y aleatorios, así como técnicas de balanceo de líneas para desarrollar operaciones más efi cientes a través de métodos cuantitativos. 

Estas 13 herramientas son muy importantes para los analistas de métodos. Los diagramas representan ayudas descriptivas y de comunicación muy valiosas para comprender un proceso y sus actividades asociadas. Su correcto uso puede ayudar a presentar y resolver el problema y en la venta e instalación de la solución. 

Las técnicas cuantitativas pueden determinar el arreglo óptimo de operadores y máquinas. Los analistas deben estar familiarizados con los conocimientos sufi cientes en álgebra y teoría de la probabilidad para desarrollar un modelo matemático que proporcione la mejor solución al problema de la máquina o de la instalación. De esta forma, ellos serán efi cientes en la presentación de métodos mejorados a la gerencia, en el entrenamiento de los empleados en el método prescrito y en el enfoque de los detalles pertinentes en conjunto con el trabajo de distribución de la planta.

BALANCEO DE LÍNEA - IX

Una gran variedad de paquetes de software disponibles en el mercado, así como herramientas de diseño, eliminan el trabajo rutinario que representa hacer los cálculos y realiza estos pasos de manera automática.

BALANCEO DE LÍNEA - VIII

Si se hace una lista de las ponderaciones posicionales en orden de magnitudes decrecientes nos da lo siguiente:

Los elementos de trabajo deben asignarse a las diferentes estaciones de trabajo. Este proceso está basado en las ponderaciones posicionales (es decir, aquellos elementos de trabajo con las ponderaciones posicionales más bajas se asignan primero) y en el tiempo del ciclo del sistema. El elemento de trabajo con el mayor peso posicional se asigna a la primera estación de trabajo. El tiempo no asignado para esta estación de trabajo se determina restando la suma de los tiempos asignados al elemento de trabajo del tiempo estimado del ciclo. Si existe tiempo no asignado, se asigna el elemento de trabajo con el siguiente peso posicional más alto, siempre y cuando los elementos de trabajo de la columna “predecesores inmediatos” ya hayan sido asignados. Una vez que se haya terminado el tiempo asignado a una estación de trabajo, el analista continúa con la estación de trabajo siguiente y el proceso también lo hace hasta que todos los elementos de trabajo hayan sido asignados.

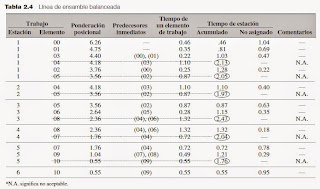
Como ejemplo, suponga que la producción requerida por turno de 450 minutos es de 300 unidades. El tiempo del ciclo del sistema es 450/300 = 1.50 minutos y la línea balanceada fi nal se muestra en la fi gura 2.4. Con relación a la confi guración que se ilustra, con seis estaciones de trabajo, tenemos un tiempo de ciclo de 1.32 minutos (estación de trabajo 4). Este arreglo produce 450/1.32 = 341 unidades, lo cual satisface el requerimiento diario de 300 unidades. Sin embargo, con seis estaciones de trabajo, tenemos también un tiempo ocioso considerable. El tiempo ocioso por ciclo es

Para lograr un balanceo más favorable, el problema puede resolverse en tiempos de ciclo menores a 1.50 minutos. Este nuevo enfoque puede traer como consecuencia la necesidad de contar con más operadores y una mayor producción diaria, la cual tendrá que ser almacenada. Otra posibilidad involucra operar la línea bajo un esquema más efi cientemente balanceado durante un número limitado de horas por día.

BALANCEO DE LÍNEA - VII

Se debe calcular una ponderación posicional por cada unidad de trabajo. Esta operación se lleva a cabo calculando la suma de la unidad de trabajo determinada y de todas las unidades de trabajo que le siguen. Por lo tanto, la ponderación posicional de la unidad de trabajo (00) sería

Figura 2.21 Matriz de precedencia utilizada en un problema de balanceo de una línea.

BALANCEO DE LÍNEA - VI

Como es evidente, a medida que hay mayor número de restricciones zonales en el sistema, serán menores las combinaciones posibles para investigación. El analista comienza con la elaboración de un bosquejo del sistema y la codifi cación de las zonas aplicables. Dentro de cada zona se muestran los elementos de trabajo que pueden elaborarse en dicha área. El analista, posteriormente, calcula el ritmo de producción mediante el uso de la expresión

donde el tiempo del ciclo del sistema es el tiempo estándar de la zona o de la estación límite. Considere otra línea de ensamblado con el diagrama de precedencia siguiente:

Este diagrama de precedencia muestra que la unidad de trabajo (00) debe terminarse antes de (02), (03), (05), (06), (04), (07), (08), (09) y (10); y que la unidad (01) debe terminarse antes de (03), (04), (07), (08), (09) y (10). Tanto (00) como (01) pueden hacerse primero, o ambas se pueden llevar a cabo de manera simultánea. Asimismo, la unidad de trabajo (03) no puede comenzar hasta que las unidades de trabajo (00) y (01) hayan terminado, y así sucesivamente. 

Para describir estas relaciones, se establece la matriz de relaciones que se muestra en la fi gura 2.21. Aquí, el número 1 signifi ca que una relación “debe preceder”. Por ejemplo, la unidad de trabajo (00) debe preceder a las unidades de trabajo (02), (03), (04), (05), (06), (07), (08), (09) y (10). También, la unidad de trabajo (09) debe preceder sólo a (10).

BALANCEO DE LÍNEA - V

Una segunda posibilidad para mejorar el balance de una línea de producción consiste en dividir un elemento de trabajo. Con referencia de nuevo a la fi gura 2.19, puede ser posible dividir el elemento H, en lugar de enviar a la estación 2 la mitad de las partes y la otra mitad a la estación 4. En muchas ocasiones no resulta económico dividir un elemento. Un ejemplo podría ser colocar ocho tornillos de máquinas con un desarmador de potencia. Una vez que el operador ha ubicado la parte en un accesorio, ha logrado controlar su herramienta y la ha puesto a trabajar, será generalmente mucho mejor poner en su lugar los ocho tornillos, en lugar de sólo hacerlo con una parte de ellos y dejar el resto a otro operador. Siempre que los elementos puedan dividirse, las estaciones de trabajo pueden balancearse mejor como resultado de la división. El procedimiento siguiente para resolver un problema de balanceo en una línea de ensamblado se basa en el método de Helgeson y Birnie (1961). El cual asume lo siguiente: 

1. Los operadores no pueden moverse de una estación de trabajo a otra para ayudar a conservar la carga de trabajo uniforme.

2. Los elementos de trabajo que se han establecido son de tal magnitud que divisiones adicionales minimizarían de forma sustancial la efi ciencia del desempeño del elemento de trabajo. (Una vez establecidos, los elementos de trabajo deben identifi carse mediante un código.)

El primer paso para solucionar el problema consiste en determinar la secuencia de los elementos de trabajo individuales. A medida que las restricciones sean menores respecto al orden en el que pueden realizarse los elementos de trabajo, mayor será la probabilidad de que se pueda lograr un balance favorable en las asignaciones laborales. Para determinar la secuencia de los elementos de trabajo, el analista contesta la pregunta siguiente: ¿Qué otros elementos de trabajo, si existen, deben terminarse antes de que este elemento de trabajo pueda comenzar? Esta pregunta se aplica a cada elemento con el fi n de establecer un diagrama de precedencia para la línea de producción que se estudia (consulte la fi gura 2.20). Un diseño funcional, la disponibilidad de métodos de producción, el espacio físico, etc., pueden presentar restricciones respecto a la secuencia de los elementos de trabajo. 

Una segunda consideración en el problema de la asignación de trabajo en una línea de producción consiste en las restricciones zonales. Una zona representa una subdivisión que puede o no estar físicamente separada o diferenciada de las demás zonas del sistema. Confi nar ciertos elementos de trabajo a una zona determinada puede justifi carse, así como congregar tareas similares, condiciones de trabajo o pago de salarios. O las restricciones zonales pueden ayudar a identifi car físicamente etapas específi cas de un componente como, por ejemplo, mantenerlo en una cierta posición mientras se llevan a cabo ciertos elementos de trabajo. Como ejemplo, todos los elementos de trabajo relacionados con un lado de un componente deben actuar en cierta zona antes de que dicho componente sea terminado.

BALANCEO DE LÍNEA - IV

Para identifi car la operación más lenta, dividimos el número estimado de operadores entre los minutos estándar asignados a cada una de las ocho operaciones. Los resultados se muestran en la tabla siguiente.

Si este ritmo de producción no es adecuado, se necesitará incrementar el ritmo de producción del operador 2, objetivo que puede lograrse mediante 1. Uno o ambos operarios trabajen en la segunda operación tiempo extra, lo que acumula un pequeño inventario en esta estación de trabajo. 2. Mediante el empleo de los servicios de un tercer operador de tiempo parcial en la estación de trabajo de la operación 2. 3. A través de la reasignación de parte del trabajo de la operación 2 a la operación 1 o a la operación 3. (Sería preferible asignar más trabajo a la operación 1.) 4. Mejorar el método en la operación 2 para reducir el tiempo del ciclo de esta operación. En el ejemplo anterior, dados el tiempo de ciclo y los tiempos de las operaciones, un analista puede determinar el número de operadores necesarios para que cada operación cumpla con un horario de producción deseado. 

El problema de la asignación de trabajo en una línea de producción también puede tener por objetivo minimizar el número de estaciones de trabajo, dado el tiempo deseado del ciclo; o, dado el número de estaciones de trabajo, asignar los elementos de trabajo a las estaciones de trabajo, dentro de las restricciones establecidas, con el fi n de minimizar el tiempo del ciclo. Una estrategia importante para balancear la línea de ensamblado consiste en compartir los de elementos de trabajo. Dos o más operadores cuyo ciclo de trabajo incluya tiempo ocioso podrían compartir el trabajo con otra estación, para hacer más efi ciente a toda la línea. 

Por ejemplo, la fi gura 2.19 muestra una línea de ensamblado que involucra seis estaciones de trabajo. La estación 1 cuenta con tres elementos de trabajo —A, B y C— para un total de 45 segundos. Observe que los elementos de trabajo B, D y E no pueden comenzar hasta que A haya terminado y que B, D y E pueden llevarse a cabo en cualquier orden. Puede ser posible compartir el elemento H entre las estaciones 2 y 4, con sólo 1 segundo de incremento del tiempo del ciclo (de 45 a 46 seg.), mientras que se ahorraron 30 seg por unidad ensamblada. Es necesario observar que compartir los elementos puede dar como resultado un aumento en el manejo del material, puesto que las partes pueden tener que ser entregadas en más de un lugar. Además, este tipo de colaboración puede implicar costos adicionales asociados con la duplicación del herramental.

BALANCEO DE LÍNEA - III

Por ejemplo, suponga que tenemos un nuevo diseño para el cual deseamos establecer una línea de ensamblado. Están involucradas ocho operaciones distintas. La línea debe producir 700 unidades diarias (o 700/480 = 1.458 unidades/minuto), y debido a que queremos minimizar el almacenamiento, no deseamos producir más de 700 unidades/día. Las ocho operaciones involucran los minutos estándar siguientes con base en datos estándares existentes: Operación 1, 1.25 minutos; operación 2, 1.38 minutos; operación 3, 2.58 minutos; operación 4, 3.84 minutos; operación 5, 1.27 minutos; operación 6, 1.29 minutos; operación 7, 2.48 minutos; y operación 8, 1.28 minutos. Para planear esta línea de ensamblado con el fi n de lograr la confi guración más económica, calculamos el número de operadores que se requieren para un nivel de efi ciencia determinado (idealmente, 100%), de la manera siguiente:

Para obtener una efi ciencia más realista de 95%, el número de operadores debe ser de 22.4/0.95 = 23.6. Puesto que es imposible tener seis décimas de operador, es necesario confi gurar la línea utilizando 24 operadores. Un método alterno sería utilizar operadores a tiempo parcial que trabajen por hora. A continuación calculamos el número de operadores que se utilizarán en cada una de las ochos operaciones específi cas. Puesto que se requieren de 700 unidades de trabajo al día, será necesario producir 1 unidad en aproximadamente 0.685 minutos (480/700). Calculamos el número de operadores necesarios para cada operación dividiendo el número de minutos permitidos para producir una pieza entre los minutos estándar para cada operación, de la manera siguiente:

BALANCEO DE LÍNEA - II

Los detalles acerca de los tiempos estándar se analizarán en el capítulo 9. Algunos analistas prefi eren considerar el tiempo ocioso en porcentaje (% ocioso):

En una situación de la vida real similar a este ejemplo, existe la oportunidad de lograr ahorros signifi cativos. Si un analista puede ahorrar 0.10 minutos en el operador 3, los ahorros totales por ciclo no son de 0.10 minutos, sino que son de 0.10 × 5, esto es, 0.50 minutos. Sólo en las situaciones más inusuales podría existir una línea perfectamente balanceada; esto es, los minutos estándar para llevar a cabo una operación serían idénticos para cada miembro del equipo. Los “minutos estándar para llevar a cabo una operación” en realidad no es un estándar. Es sólo un estándar para la persona que lo estableció. Por lo tanto, en nuestro ejemplo, donde el operador 3 tiene un tiempo estándar de 0.65 minutos para llevar a cabo la primera operación, un analista de medición de trabajo diferente pudo haber asignado un valor tan pequeño como 0.61 minutos o tan grande como 0.69 minutos. 

El rango de estándares establecidos por diferentes analistas de medición del trabajo acerca de la misma operación puede ser aún mayor que el rango sugerido. La cuestión es que ya sea que el estándar generado haya sido de 0.61, 0.65 o 0.69, el operador típico consciente debió haber tenido un poco de difi cultad para cumplir con el estándar. De hecho, el operador probablemente mejorará el estándar en vista del desempeño de los operadores de la línea con menor contenido de trabajo en sus asignaciones. Los operadores que tienen un tiempo de espera basado en la producción del operador más lento casi nunca están esperando. En lugar de eso, reducen el tiempo de sus movimientos para utilizar el número de minutos estándar establecido por el operador más lento. El número de operadores necesarios para fi jar la velocidad de producción requerida puede calcularse mediante

BALANCEO DE LÍNEA - I

El problema de determinar el número ideal de operadores que se deben asignar a una línea de producción es análogo al que se presenta cuando se desea calcular el número de operadores que se deben asignar a una estación de trabajo; el diagrama de procesos de grupo resuelve ambos problemas. Quizá la situación de balanceo de línea más elemental, que se encuentra muy a menudo, es uno en el que varios operadores, cada uno de los cuales lleva a cabo operaciones consecutivas, trabajan como si fueran uno solo. En dicha situación, la velocidad de producción depende del operador más lento. 

Por ejemplo, tenemos una línea con cinco operadores que ensamblan montajes de hule enlazados antes de entrar al proceso de curado. Las tareas específi cas del trabajo podrían ser las siguientes: Operador 1, 0.52 minutos: operador 2, 0.48 minutos; operador 3, 0.65 minutos; operador 4, 0.41 minutos; operador 5, 0.55 minutos. El operador 3 establece el paso, como lo evidencia lo siguiente:

La efi ciencia de esta línea puede calcularse como la relación entre la cantidad de minutos estándar reales y el total de minutos estándar permitidos, es decir

EJEMPLO - Cálculo de la interferencia entre máquinas mediante el uso del método de Ashcroft

En referencia al ejemplo 2.3:

De la tabla A3-13, del apéndice 3, con tiempo de servicio exponencial y k = 0.02 y N = 60, tenemos un tiempo de interferencia entre máquinas de 16.8% del tiempo del ciclo. Tenemos Ti = 0.168c, donde c es el tiempo del ciclo para producir una unidad por eje. Entonces,

El tiempo de interferencia calculado mediante la ecuación (34.8 minutos, ejemplo 2.3) coincide en buena medida con el desarrollado aquí mediante el modelo de la teoría de colas. Sin embargo, a medida que n (el número de máquinas asignadas) es menor, la diferencia proporcional entre las dos técnicas aumenta.

RELACIONES COMPLEJAS - II

Mediante el uso de la teoría de colas, y bajo el supuesto de que el lapso de tiempo entre los tiempos muertos tiene una distribución exponencial, Ashcroft (1950) extendió el método anterior y desarrolló tablas para determinar los tiempos de interferencia de las máquinas. Dichos tiempos se muestran en la tabla A3-13 (apéndice 3) y proporcionan valores de tiempo de operación de las máquinas y de tiempo de interferencia entre ellas para valores de la relación de servicio k:

Observe que los valores del tiempo de operación de la máquina y el tiempo de interferencia entre máquinas de la tabla A3-13 están dados como porcentaje del tiempo total del ciclo. Además, cualquier tiempo de desplazamiento o tiempo de trabajador w debe incluirse como parte del tiempo de servicio. El ejemplo 2.4 muestra el método de Ashcroft para calcular el tiempo de interferencia con las máquinas.

EJEMPLO - Cálculo del tiempo de interferencia con las máquinas

En la producción de plumas, a un operador se le asignan 60 ejes. El tiempo promedio de operación de la máquina por paquete, determinado mediante un estudio con cronómetro, es de 150 minutos. El tiempo promedio estándar de servicio por paquete, también desarrollado mediante un estudio de tiempos, es de 3 minutos. El cálculo de la interferencia con la máquina, expresado como un porcentaje del tiempo promedio de atención del operador es

RELACIONES COMPLEJAS - I

Las combinaciones de servicio sincrónico y aleatorio son quizás el tipo más común de relación entre operador y máquina. En este caso, el tiempo de servicio es relativamente constante, a pesar de que las máquinas son operadas de manera aleatoria. Además, se supone que el tiempo entre fallas tiene una distribución particular. 

A medida que el número de máquinas aumenta y la relación entre el operador y la máquina se hace más compleja, la interferencia con la máquina y, como consecuencia, el tiempo de retardo, aumentan. En la práctica, la interferencia con la máquina predominantemente representa de 10 a 30% del tiempo total de trabajo, con valores extremos de hasta 50%. Se han desarrollado varios métodos para lidiar con dichas situaciones. 

Uno de ellos supone una carga de trabajo esperada por el operador basada en el número de máquinas asignadas y en los tiempos promedio de operación de las máquinas y los tiempos promedios de servicio. Para un total de hasta seis máquinas, se recomienda el uso de las curvas empíricas que se muestran en la fi gura 2.18. Para siete o más máquinas, puede utilizarse la fórmula de Wright (Wright, Dubai y Freeman, 1936):

SERVICIO ALEATORIO - EJEMPLO - Servicio aleatorio

Un operador debe dar servicio a tres máquinas que tienen un tiempo fuera de servicio esperado de 40%. Cuando está trabajando, cada máquina puede producir 60 unidades/hora. Al operador se le paga $10.00/hora y una máquina cuesta $60.00/hora. ¿Vale la pena contratar a otro operador para que mantenga a las máquinas en operación?

Por lo tanto, es más efi ciente desde el punto de vista económico contratar a otro operador y mantener las máquinas en operación. Observe que contratar a un tercer operador para mantener las tres máquinas operando todo el tiempo no sería efi ciente desde el punto de vista de las economías que se podrían obtener. Aunque la producción total aumenta marginalmente, el costo total aumenta más y el costo unitario se calcula como sigue

TEC  13  10  3  602>180  $1.17>unidad

SERVICIO ALEATORIO - II

Mediante el uso de este método puede determinarse la proporción del tiempo en la que algunas máquinas estarán fuera de servicio y el tiempo perdido resultante de un operador de tres máquinas puede calcularse fácilmente. En este ejemplo, tenemos lo siguiente:

Se pueden hacer cálculos similares en el caso de más o menos asignaciones de máquinas, con el fi n de determinar la asignación que da como resultado el menor tiempo fuera de servicio de éstas. La asignación más satisfactoria es generalmente la confi guración que tenga el menor costo total esperado por pieza, mientras que el costo esperado total por pieza de una confi guración dada se calcula mediante la expresión

La velocidad de producción, en piezas por hora, de n máquinas se calcula con el tiempo promedio de máquina que se requiere por pieza, el tiempo promedio de servicio de máquina por pieza y el tiempo muerto esperado o tiempo perdido por hora. Por ejemplo, con la ayuda de un operador al que se le han asignado cinco máquinas, un analista puede determinar que el tiempo de maquinado por pieza fue de 0.82 h, el tiempo de servicio a la máquina por pieza fue de 0.17 horas y el tiempo perdido por máquina fue en promedio de 0.11 horas por hora. Por lo tanto, cada máquina estuvo disponible para realizar trabajo productivo solamente 0.89 horas cada hora. El tiempo promedio que se necesita para producir una pieza por máquina será de

Por lo tanto, las cinco máquinas producirán 4.5 piezas por hora. Con un costo operador-hora de $12 y un costo hora-máquina de $22, tenemos un costo total esperado por pieza de

SERVICIO ALEATORIO - I

Las situaciones de servicio totalmente aleatorio son aquellos casos en los que no se conoce cuándo se debe proporcionar servicio o cuánto tiempo dura el servicio a un equipo. Por lo general, los valores promedio se conocen o pueden ser determinados; con dichos promedios, las leyes de probabilidad pueden proporcionar una herramienta útil para determinar el número de máquinas que se debe asignar a un solo operador. Los términos sucesivos de la expansión binomial proporcionan una aproximación útil de la probabilidad de 0, 1, 2, 3,…, n máquinas fuera de operación (donde el valor de n es relativamente pequeño), suponiendo que cada máquina está fuera de servicio en tiempos aleatorios durante el día y que la probabilidad de que estén fuera de servicio sea p y la probabilidad de que estén en operación sea q = 1 – p. Cada término de la expansión binomial puede representarse como una probabilidad m (de n) máquinas fuera de servicio:

Como ejemplo, determinemos la proporción mínima de tiempo de máquina perdido de varios tornos de torreta asignados a un operador donde la máquina promedio trabaja sin prestársele atención 60% del tiempo. El tiempo de atención del operador (la máquina está fuera de servicio o requiere servicio) a intervalos irregulares es 40% en promedio. El analista estima que deben asignarse tres tornos de torreta por operador en este tipo de trabajo. En esta confi guración, la probabilidad de que m (de n) máquinas estén fuera de servicio será como sigue: