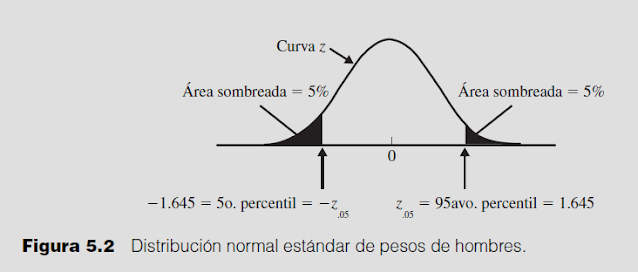
para formar una distribución normal estándar (también llamada distribución z; vea la fi gura 5.2).
Una vez normalizada, cualquier distribución de población cuya forma se aproxime a la de una
campana tendrá las mismas propiedades estadísticas. Esto permite un cálculo fácil de cualquier valor
percentil deseado, mediante el uso de los valores k y z apropiados, de la manera siguiente:
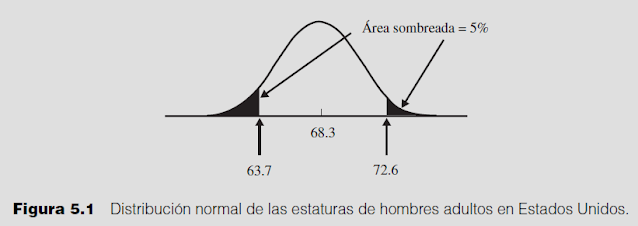
Como la estatura media de los hombres en Estados Unidos es de 68.3 pulgadas (173.6 cm), mientras
que la desviación estándar es de 2.71 pulgadas (6.9 cm)(Webb Associates, 1978), el 95avo. percentil
de la estatura de los hombres se calcula como
68.3 + 1.645(2.71) = 72.76 pulgadas
mientras que el 5o. percentil de la estatura de los hombres es
68.3 - 1.645(2.71) = 63.84 pulgadas
Observe que los valores calculados 72.76 y 63.84 no son exactamente iguales a los valores reales de
72.6 y 63.7 pulgadas. Esta diferencia se debe a que la distribución de estaturas de los hombres en
Estados Unidos no es una distribución totalmente normal.

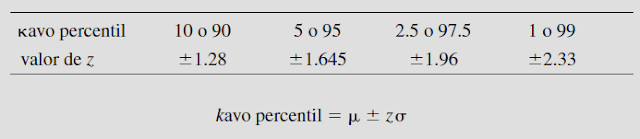
No hay comentarios:
Publicar un comentario